Algorithms
Drawing circles - Jesko's-Method
So far "Fastest Algorithm Drawing Rasterized Circles"
Preface
I developed a superior (in terms of “less-operations”) “Circle-Algorithm” in 1985/1986.
This now is a gift to the community.
Enjoy!
PreKnowledge, PriorArt
From Wikipedia (I cite it because the description have several algorithms in common):
The objective of the algorithm is to approximate the curve using pixels; Every pixel should be approximately the same distance from the center.
At each step, the path is extended by choosing the adjacent pixel which satisfies but maximizes . Since the candidate pixels are adjacent, the arithmetic to calculate the latter expression is simplified.
using pixels; Every pixel should be approximately the same distance from the center.
but maximizes 
. Since the candidate pixels are adjacent, the arithmetic to calculate the latter expression is simplified.These algorithms
- … draw all eight octants simultaneously, starting from each cardinal direction (0°, 90°, 180°, 270°) and extend both ways to
reach the nearest multiple of 45° (45°, 135°, 225°, 315°). They can determine where to stop because when y = x, they have reached 45°.
Start (at iteration #0) of all 8 pixels is easy to find (laying on one axis). If drawing 8 pixels around the origin ( midpoint=( 0; 0 ) ): ( x; 0 ), ( x; 0 ), ( -x; 0 ), ( -x; 0 ), ( y; 0 ), ( y; 0 ), ( -y; 0 ), ( -y; 0 ). Don’t wonder: In the first iteration 4 pixels are duplicates. - … work iterativly.
- … depend in their performance difference only on number of calculculations done to get the next pixel position.
Motivation
History
Decades ago in 1985, I experimented with Bresenhams line algorithm as a pupil on my Commodore 64 (I still love it). Without the Internet and relevant literature I was limited in all directions having only my C64 and some bit-knowledge, knowing how to optimize my assembler programs. In these times an extremly fast line subroutine was created by me drawing from both sides, taking in account the octants, reducing conditionals, saving in between results etc. 35k points per second on a machine capable of doing about ~490k operations per second, this is 14 operations (max.) per pixel including address calculation and bit operations to set it finally.
This was “Line-Algorithm”, but my circles I drew calculating points with sin/cos and drawing with these quick lines in between. Later with some square-root function …
My problem was a mixture of missing accuracity and speed. I didn’t want to accept, that lines could by drawn such fast and accurate, but circles not.
The experiment ...
So I experimented with my line algorithm … after reordering some variables, trying here and there I destroyed somehow the line algorithm, but I got an interesting figure:
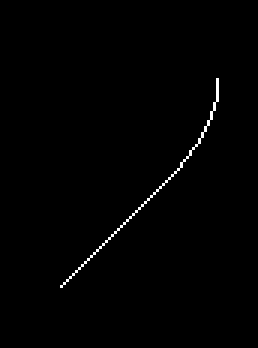
As one could see there is something circular and a straigt line in 45° down to the lower left. Looking at the code I couldn’t understand it directly, but what I found out relatively quick was to kill the straigt line extension. I compared two variables for equality and stopped my loop then.
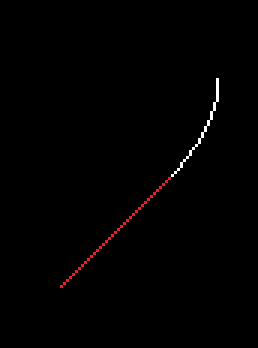
Finally:
This looked like a perfectly drawn circle on a raster display 🙂
Comparison of Methods
Beside Bresenham some others have tried to draw circles on raster displays and plotters.
Method of Horn
If we want to estimate the performance, we can concentrate on counting the arithmetic operations which are part of the loop:
- ( y > x ): 1 Operation – substraction
- Pixel(): 0 Operation
- d = d + 2 * y + 1: 3 Operations – 2 additions and a shift or 3 additions
- y++: 1 Operation – addition
- ( d > 0 ): 1 Operation – substraction (use of >= 0 would only be check only sign bit)
- d = d – 2 * x + 2: 3 Operations – 1 substraction, 1 additions, a shift and an addition or 1 substraction, 2 additions
- x–: 1 operation – 1 substraction
d = −r
x = r
y = 0
Repeat until y > x
Pixel (x, y) and symmetrical pixel are colored
d = d + 2×y + 1
y++
If d > 0
d = d - 2×x + 2
x-- Midpoint Method
If we want to estimate the performance, we can concentrate on counting the arithmetic operations which are part of the loop:
- ( x > y ): 1 Operation – substraction
- Pixel(): 0 Operation
- y++: 1 Operation – addition
- ( P <= 0 ): 1 Operation – substraction
- P = P + 2*y + 1: 3 Operations – 2 additions and a shift or 3 additions
- x–: 1 Operation – 1 substraction
- P = P + 2*y + 1 – 2*x: 2 (additional) operations (-2x) – 1 substraction and shift or 2 substractions
Count of operations: 9
x = r
y = 0
P = 1 - r
while ( x > y )
Pixel (x, y) and symmetrical pixel are colored
y++
if ( P <= 0 )
// Mid-point is inside or on the perimeter
P = P + 2*y + 1
else
// Mid-point is outside the perimeter
x--
P = P + 2*y - 2*x + 1
Jesko's Method
If we want to estimate the performance, we can concentrate on counting the arithmetic operations which are part of the loop:
- ( y >= x ): 1 Operation – substraction
- Pixel(): 0 Operation
- y++: 1 operation – addition
- t1 += y: 1 Operation – addition
- t2 = t1 – x: 1 Operation – substraction
- ( t2 >= 0 ): 0 Operation – (check only sign bit)
- t1 = t2: 0 Operations
- x–: 1 operation – 1 substraction
y = 0;
t1 = r >> 4;
x = r;
while ( x >= y ) // 1st op
Pixel (x, y) and symmetrical pixel are colored
y++ // 2nd op
t1 += y // 3rd op
t2 = t1 - x // 4th op
if ( t2 >= 0 ) // does not count, no calculation, only positive check from result above
t1 = t2 // does not count either, register swap or similar
x-- // 5th op
Thougths
As I already told, I wasn’t aware of it @1985/86. I simply had to use my brain and eyes.
Looking back now reveals that some activities happened, but I still do not know, whether my algorithm is “beaten” in some way (less operations per 8 pixels). Maybe this can be clarified by my publication to the community now.
Basically this arithmetic progression is used:
n² = 1 + 3 + 5 + 7 + … + (2n – 1 )
Making algorithms fast means for normal, that we have less to calculate or less memory accesses. In the case of the circles I want to show here, that we only have less mathematical operations or can use meta information of already done calculations to hint/support other calculations.
Impact on current hardware is probably low, but maybe it helps to save transistors, FPGA space, keeps on living on embedded systems, or simply can show how algorithms may be optimized to a minimum of operations.
Thanks for reading!
/Jesko Schwarzer
2022-Feb-13
Publications
Appendix: Small C-Program
Here a small C-Program. Store the text as “main.c” and compile it. It outputs the coordinates of a circle with radius 10.
#include <stdio.h>
void
plot( int x, int y )
{
printf( "x=%3d, y=%3d\n", x, y );
}
void
circle( int mx, int my, int r )
{
int t1 = r / 16;
int t2 = 0;
int x = r;
int y = 0;
while ( x >= y )
{
plot( mx + x, my + y );
plot( mx + x, my - y );
plot( mx - x, my + y );
plot( mx - x, my - y );
plot( mx + y, my + x );
plot( mx + y, my - x );
plot( mx - y, my + x );
plot( mx - y, my - x );
y = y + 1;
t1 = t1 + y;
t2 = t1 - x;
if ( t2 >= 0 )
{
t1 = t2;
x = x - 1;
}
}
}
int
main()
{
circle( 20, 30, 10 );
return 0;
}
Visits: 1504